M&A Blog #20 – valuation (Dividend Discount Model - DDM)

For this valuation post, I wanted to talk about a valuation method that is making its way out of academia and into the real world, a method that is gaining popularity in the world of portfolio management. As I mentioned in my valuation preparation post, Dividend Discount Model (DDM) is a valuation method that uses the predicted dividends and a discount rate to find the present value estimate of a potential investment. In this post, we will discuss the mechanics of DDM step by step, starting from the point where all the needed tools and data for such analysis as outlined here have been gathered.

The major steps of DDM are:

1. Deriving the proper discount rate (rate of return).

2. Deciding on a forecast horizon (holding period).

3. Deriving the long-term dividend growth rate.

4. Forecasting dividend amounts during the forecast horizon, as well as their present values.

5. Forecasting the future stock price at the end of the forecast horizon, as well as its present value.

6. Performing sensitivity / scenario analysis using Monte Carlo analysis.

We will delve deeper into each steps above in the following paragraphs of this post. It is worth noting that each step can justifiably warrant an entire post in itself. For the purposes of this post though, we will keep matters concise by discussing only the most practical and commonly accepted aspects of each step.

The 1st step in DDM is to derive the proper discount rate (Rate of Return). Because dividends is a piece of equity, we can use the Capital Asset Pricing Model (CAPM) to calculate the proper Rate of Return (r). All we need are the risk-free rate, the market risk premium, and the target’s beta; which fortunately, we already gathered. The next (2nd) step in this method calls for the determination of a forecast horizon (holding period). For the purpose of this exercise, let’s call it 15 years (one can choose a much shorter horizon of 5, 10, etc. years).

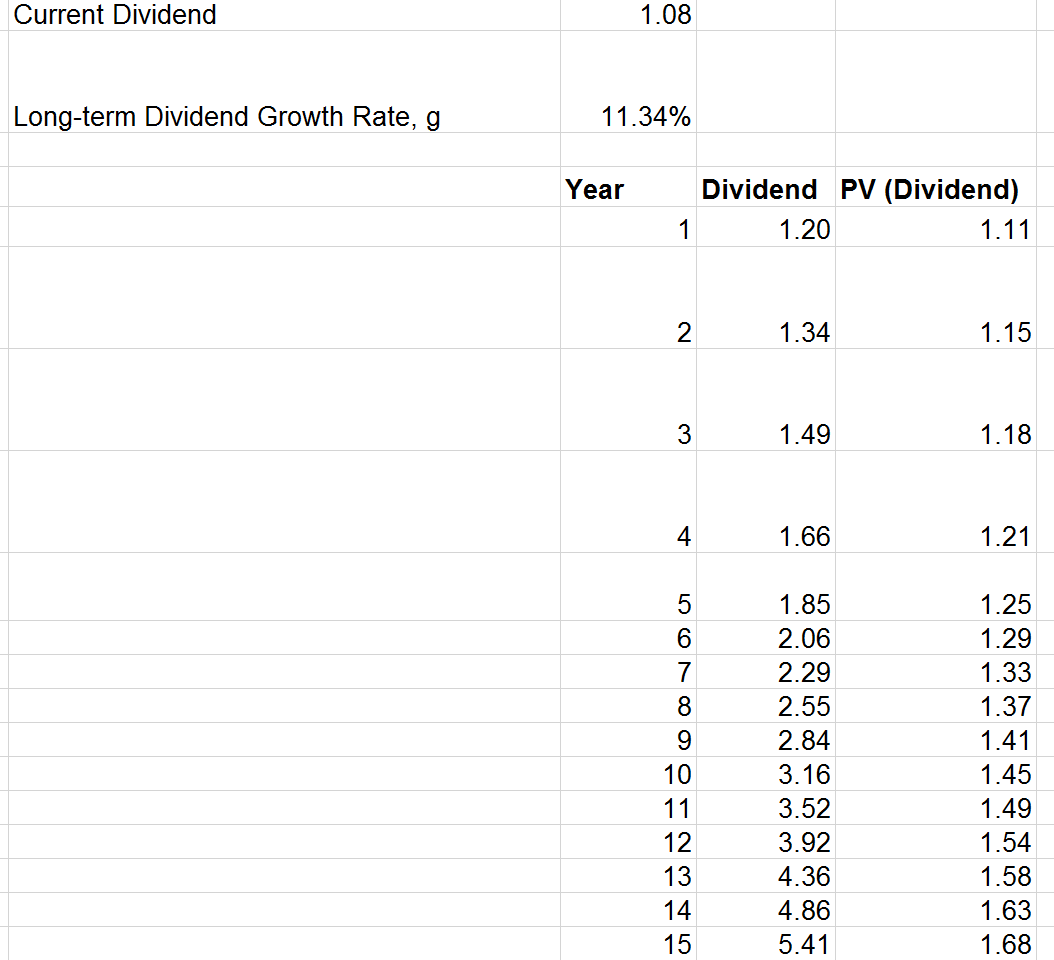
The 3rd step in DDM is to calculate the long-term dividend growth rate. For this calculation, we would need the target’s dividend history, preferably over the same backward period as the length of our forecast horizon. We calculate the growth rate as follow:

• Long-term dividend growth rate (g) = (the most recent dividend / the dividend at the start of the historical period) ^ (1/the number of lapsing years) - 1.

  • Note that the number of lapsing years here would 14 (from the number of years between the first year dividend to the 15th year dividend).

The next (4th) step in DDM calls for the forecasting of dividend amounts during the forecast horizon, as well as their present values. For this part, we simply calculate:

• Dividend = Prior Year Dividend * (1 + Long-term Dividend Growth Rate).

• Present Values of Dividend = PV (Dividend) = Dividend / (1 + Rate of Return) ^ the number of years into the future.

• We should have 15 Dividend amounts and 15 PV (Dividend) amounts at this point.

The 5th step in DDM is a bit more complex. It is the forecasting of future stock price at the end of the forecast horizon along with its present value calculation. To perform this forecast, we need the target’s dividend history again, the book value of equity and year-end shares outstanding, and the stock prices at year-end. Fortunately, we have gathered the data as outlined here. We proceeded with the calculation as follow:

• Market Price at year-end (of the target) = Year-end Shares Outstanding * Stock Price at year-end.

• Market Price as multiple of Book Value of Equity at year-end = Market Price at year-end / Book Value of Equity.

• Average (mean) of the market multiples = from the last 5 years (or a reasonable length of period).

• Projected Book Value of Equity at the end of the 15 years = from the proforma balance sheet that we developed in our DCF post.

• Projected Market Price at the end of the 15 years = Average (mean) of the market multiples * Projected Book Value of Equity at the end of the 15 years.

• Projected number of shares at the end of the 15 years = The average of shares outstanding from recent historical financials, assuming consistency over recent years.

• Projected Share Price at the end of the 15 years = Projected Market Price at the end of the 15 years / Projected number of shares at the end of the 15 years.

• Present Value of Projected Share Price at the end of the 15 years = PV (Projected Share Price) = Projected Share Price / (1 + Rate of Return) ^ the number of years into the future.

  • We should have 1 Projected Share Price and 1 PV (Projected Share Price) at this point.

The 6th and final step in a proper DDM method is to perform sensitivity / scenario analysis, preferably using a Monte Carlo simulation. Because this step is similar in this method as it is in the other valuation methods (DCF, Comparable Company, etc.), we will discuss sensitivity / scenario analysis in great details in the last post of this valuation series in 1-2 posts from now.

A sample file for a DDM analysis on the company McKesson can be accessed here; it is recommended to open @RISK first before opening this file due to the Monte Carlo simulation embedded in this file (the file will open with errors without @RISK). To download @RISK for a free trial version, click here.

As we can tell from the steps laid out thus far, DDM has advantages and disadvantages. The advantages include its simplicity and usage of dividends (which is a signal for profitability). DDM’s disadvantages include the fact that it can only be used with companies who pay dividends regularly (i.e. mature, profitable companies). The model doesn’t work with companies who don’t pay dividends or don’t pay dividends regularly (when dividends are not tied to profitability).

So, to recap, we have discussed the development of a DDM model and its supporting elements, along with its strengths and weaknesses. Given its advantages and disadvantages, DDM is best used in conjunction with other valuation methods (like DCF and Comparable Company). It is only then that the closest-to-correct value of the target can be deduced via comparison. In the next post, we will discuss scenario / sensitivity analysis using Monte Carlo simulation.